5.1. Общая характеристика растворов
Истинным раствором называется гомогенная система, состоящая из двух и более компонентов. Растворы бывают жидкие, твердые и газообразные. Истинные растворы термодинамически устойчивы. Их образование самопроизвольно, т.е. в процессе растворения вещества в растворителе энергия Гиббса системы уменьшается (ΔGобразования<0). Компонент, преобладающий по составу, называют растворителем, остальные компоненты – растворенные вещества.
Важнейшей характеристикой раствора является его концентрация. В теории растворов ее обычно выражают следующими тремя способами.
1. Молярность: С, М – это количество молей растворенного вещества в литре раствора.
2. Моляльность: m – количество молей растворенного вещества в 1000 г растворителя.
3. Молярная доля: N - количество молей данного вещества, отнесенное к сумме чисел молей всех компонентов раствора.
Все растворы по свойствам делят на три группы: идеальные, предельно разбавленные и неидеальные (реальные).
Идеальным называется раствор, образование которого из компонентов не сопровождается тепловым эффектом и изменением объема: ΔН=0, ΔV=0. В идеальном растворе энергии взаимодействия всех видов молекул одинаковы.Такие растворы образуют, например, соседние гомологи в ряду органических соединений или смеси изомеров.
Предельно разбавленным называется раствор, в котором концентрация растворенного вещества бесконечно мала.Растворитель в таких растворах подчиняется законам идеальных растворов, а растворенные вещества не подчиняются.
Неидеальными называются растворы, которые не подчиняются законам идеальных и предельно разбавленных растворов.Для характеристики их равновесных свойств пользуются методом активности (Г. Льюис).
Равновесные свойства раствора зависят от состава раствора и свойств его компонентов. Эти зависимости устанавливаются термодинамической теорией растворов. Свойства компонентов раствора выражаются через парциальные молярные величины.
5.2. Парциальные молярные величины
Вводя понятие «химический потенциал», мы познакомились уже с одной парциальной молярной величиной. Это парциальный молярный изобарный потенциал, который тождественен понятию химический потенциал компонента раствора [уравнение (2.68)]:
mi º  =
= 
Изобарный потенциал – это экстенсивное свойство, т.е. величина его зависит от количества, массы вещества. Экстенсивными свойствами раствора являются также энтальпия, энтропия, объем, теплоемкость. Обозначим любое из этих термодинамических свойств раствора -X.Для двухкомпонентного раствора:
X= f(P,T,n1, n2) , (5.1)
где n1 – число молей растворителя, n2 – растворенного вещества.
Поскольку G, Н, S являются функциями состояния системы, то полный дифференциал от этого выражения при постоянных Р и Т:
 (5.2)
(5.2)
Обозначим 
тогда
 (5.3)
(5.3)
- свойство i-го компонента в растворе, называемое парциальной молярной величиной.
Парциальной молярной величиной называют отношение бесконечно малого изменения экстенсивного свойства раствора к бесконечно малому приращению количества данного компонента в растворе при постоянстве Р, Т и числа молей второго компонента.
При помощи парциальных молярных величин можно оценить вклад каждого компонента в экстенсивное свойство раствора.
Проинтегрируем уравнение (5.3) при условии постоянства состава раствора. При этом n1 меняется от 0 до n1, а n2 от 0 до n2. Так как парциальные молярные величины зависят не от количества раствора, а от соотношения компонентов, то при интегрировании их можно рассматривать как постоянные величины. X раствора при этом изменится от 0 до X:
 (5.4)
(5.4)
Продифференцируем (5.4), считая все величины переменными:
 (5.5)
(5.5)
Сравнив (5.5) и (5.3), получим
 (5.6)
(5.6)
Для i-компонентной системы:
 (5.7)
(5.7)
Если оба слагаемых в (5.4) и (5.6) или каждое слагаемое в (5.7) разделить соответственно на (n1+n2) или на Σni, то получим
(5.8)
(5.9)
 , (5.10)
, (5.10)
где N1, N2, Ni – молярные доли компонентов.
Уравнения (5.4) – (5.10) называются уравнениями Гиббса – Дюгема.
Они связывают парциальные молярные величины с составом раствора.
Чаще всего в качестве X мы будем использовать химический потенциал μ:
N1dμ1 + N2dμ2 = 0(5.11)
Из (5.11) выразим dμ1:
dμ1 = -  μ2 (5.12)
μ2 (5.12)
Это уравнение часто применяют к пару, находящемуся в равновесии с раствором. Если пар – идеальная газовая смесь, то
mi=mi0 + RTlnPi .
Подставив последнее в (5.12), получим:
RTdlnP1 = -  RTdlnP2 или
RTdlnP2 или
dlnP1 = -  dlnP2 (5.13)
dlnP2 (5.13)
Это уравнение называется уравнением Дюгема – Маргулеса. Мы будем применять его для вывода закономерностей, описывающих поведение растворов.
В уравнении (5.8) зависимость X от N2 не линейна, так как  и
и  зависят от состава раствора. Поэтому свойство раствора X в общем случае является не аддитивной величиной. Для аддитивного свойства:
зависят от состава раствора. Поэтому свойство раствора X в общем случае является не аддитивной величиной. Для аддитивного свойства:
Xадд = N1X1º + N2X2º (5.14)
X1º и X2º - свойства одного моля растворителя и растворенного вещества в чистом виде.
Далее мы перейдем к рассмотрению термодинамических свойств растворов, перечисленных в начале главы.
5.3. Давление насыщенного пара компонента над раствором. Законы Рауля и Генри. Растворимость газов в жидкостях
Условие равновесия i –компонента в растворе и паре выражается равенством химических потенциалов компонента в растворе μi и в паре μi‘
μi = μi‘
Если пар подчиняется законам идеальных газов, то
μi‘ = μiº + RTlnPi и
dμi = RTdlnPi ,
отсюда
dlnPi =  (5.15)
(5.15)
если 1 – растворитель, а 2 – растворенное вещество, то
dlnP1 = ; dlnP2 = (5.16)
где Р1 – парциальное давление пара растворителя над раствором;
Р2 – парциальное давление пара растворенного вещества над раствором;
Р1 + Р2 = Р – общее давление пара над раствором.
Поскольку существуют отличия в поведении идеальных, предельно разбавленных и реальных растворов, будем рассматривать далее закономерности в поведении каждой из этих групп в отдельности.
А) Идеальные растворы
Химический потенциал каждого из двух компонентов идеального раствора (1 – растворитель, 2 – растворенное вещество) выражается уравнением:
μi = μiº + RT lnNi
и
dμi = RTdlnNi (5.17)
подставим (5.17) в (5.15):
dlnPi = dlnNi (5.18)
Проинтегрируем (5.18) от Рiº до Рi и от Ni = 1 до Ni :
 (5.19)
(5.19)
Отсюда Рi = PiºNi (5.20)
Уравнение (5.20) называют уравнением Рауля. В идеальном растворе оно применимо и к растворителю, и к растворенному веществу. В соответствии с уравнением (5.20), равновесное парциальное давление пара компонента над раствором равно произведению давления пара над чистым компонентом Рiº на его молярную долю в растворе.
Уравнение (5.20) справедливо при постоянной температуре.
Общее давление пара над раствором равно сумме парциальных давлений:
Р = P1ºN1 + P2ºN2 = Р1º(1-N2) + P2ºN2
или
Р= P1º - N2(P1º - P2º) (5.21)
Уравнения (5.20) и (5.21) являются уравнениями прямых в координатах Р1 – N1 , P2 – N2 , P – N2 , где Ni – состав раствора.
Представим эти зависимости графически, рис.5.1.
Здесь общее давление пара выражено как функция состава раствора. Если выразить общее давление пара над раствором как функцию состава пара, то получим гиперболическую кривую пара, P=f(N2‘ ), лежащую ниже, чем кривая жидкости, P=f(N2), рис. 5.2.

Рис. 5.1. Зависимости общего и парциальных давлений от состава идеального раствора

Рис. 5.2. Диаграмма «состав – давление пара» для жидкой бинарной летучей смеси, подчиняющейся законам идеальных растворов
Такая диаграмма называется диаграммой «состав -давление пара». Над кривой жидкости – область жидкости. Под кривой пара – область ненасыщенного пара. Между кривыми – область гетерогенного равновесия жидкость↔пар. Возьмем точку М в гетерогенной области и проведем линию, параллельную оси абсцисс, до пересечения с кривыми жидкости и пара (она называется нода). Полученные точки на кривых характеризуют составы сопряженных фаз: жидкости и насыщенного пара при данной температуре. Как видно из графика, пар относительно богаче равновесной с ним жидкости более летучим компонентом, в данном случае – вторым. Это различие в составах жидкости и пара устанавливается первым законом Коновалова: «Пар над смесью двух летучих жидкостей относительно богаче тем компонентом, добавление которого к жидкости повышает общее давление над раствором при постоянной температуре или понижает температуру кипения раствора при постоянном давлении».
Как будет показано далее, первый закон Коновалова выполняется и в реальных, неидеальных растворах. Это различие в составах жидкости и пара используется для разделения летучих смесей перегонкой (см. раздел 5.5).
Б) Предельно разбавленные растворы
В предельно разбавленном растворе закон Рауля применим только к растворителю:
Р1 = Р1ºN1,
что легко преобразуется к виду:
Р1º - Р1 = Р1º - Р1ºN1, или , где Р1º-Р1 =ΔР1 – понижение давления пара растворителя над раствором. Тогда
 ,(5.22)
,(5.22)
т.е. относительное понижение давления пара растворителя над раствором пропорционально молярной доле растворенного вещества. Это утверждение, а также его математическая запись (5.22) называется первым законом Рауля.
К растворенному веществу в предельно разбавленных растворах закон Рауля не применим, а применим закон Генри:
Р2 = КгN2 , (5.23)
т.е. парциальное давление пара растворенного вещества над предельно разбавленным раствором пропорционально молярной доле растворенного вещества. Величина Кг называется константой Генри (или коэффициентом Генри). Но Кг ≠ Р2º, а определяется экстраполяцией опытных данных:
 (5.24)
(5.24)
Закон Генри установлен опытным путём для растворов газов в жидкостях. Растворимость газов в жидкостях определяет многие процессы и имеет поэтому большое практическое значение.
Если растворенное вещество – газ, то в уравнении (5.24) N2 представляет собой растворимость газа в жидкости при парциальном давлении этого газа над раствором Р2. Таким образом, из уравнения Генри следует, что растворимость газов в предельно разбавленных растворах пропорциональна их парциальному давлению над раствором.Количество растворенного газа чаще выражают не в молярных долях, а в единицах объёма:
VT = K·P2 , (5.25)
где К – коэффициент растворимости; VT – объём газа при температуре Т. Коэффициент растворимости – это объём газа, который растворяется при данной температуре в единице объёма растворителя при парциальном давлении газа, равном единице.Если Т=273К, то уравнение (5.25) выражают через коэффициент поглощения газа Кп:
V273 = Кп·Р2 , (5.26)
где V0 – объём газа, который растворяется в единице объёма растворителя при температуре 273К.
В присутствии электролитов растворимость газов уменьшается. Это явление называется высаливанием. И.М. Сеченовым получено эмпирическое уравнение, описывающее этот процесс количественно:
 , (5.27)
, (5.27)
где С0Г – растворимость газа в воде, СГ - растворимость газа в растворе электролита; СЭ – концентрация электролита.
Высаливающий эффект электролита тем больше, чем больше заряд ионов электролита и меньше их радиус: NaCl<MgCl2<AlCl3. Высаливающий эффект объясняется гидратацией ионов в растворе. Взаимодействия растворитель – ион связывают часть растворителя, поэтому ослабляется взаимодействие растворитель – газ, и растворимость газов падает. Поэтому растворимость газов в морской воде меньше, чем в речной. Например, растворимость О2 в морской воде, в зависимости от солёности, от 0 до 9 мл/л; N2 – 8,4-14,5 мл/л, при 0оС.
В) Неидеальные (реальные) растворы. Отклонения
от закона Рауля
В реальных растворах закон Рауля не выполняется. Зависимости парциальных давлений компонентов от состава раствора не линейны и выражаются через активности компонентов в растворе аi , зависящие от концентрации и свойств компонентов:
Р1 = Рº1 а1 ; Р2 = Рº2 а2 (5.28)
Наблюдаются положительные и отрицательные отклонения от закона Рауля в реальных растворах. Они обусловлены различными взаимодействиями между однородными и разнородными молекулами в растворе. Если однородные молекулы притягиваются друг к другу сильнее, чем разнородные, то это облегчает переход молекул в газовую фазу и давление повышается. Диаграмма «давление – состав жидкости» в этом случае имеет вид рис. 5.3.
Примерами таких растворов являются бензол – ацетон, вода - метиловый спирт. Их образование сопровождается поглощением тепла.
Если сильнее взаимное притяжение разнородных молекул ( сольватация, водородные связи и т.п.), то переход молекул в газовую фазу затруднён. Давление пара ниже, чем в идеальных системах, наблюдаются отрицательные отклонения от закона Рауля (рис. 5.4).
Образование таких растворов сопровождается выделением тепла. Это, например, хлороформ и ацетон.
Если отклонения от закона Рауля велики, то на кривой «давление – состав» появляется экстремум: максимум или минимум, рис.5.5.


Рис. 5.3., 5.4. Диаграммы «давление – состав жидкости» при положительных и отрицательных отклонениях от закона Рауля.

а) б)
Рис. 5.5. Кривые «давление – состав жидкости» при больших положительных (а) и отрицательных (б) отклонениях от закона Рауля
5.4. Диаграммы «давление - состав», «температура – состав» и законы Коновалова для реальных систем
Диаграммы «давление – состав» для реальных растворов без экстремума и с экстремумом изображены в верхнем ряду рис. 5.6. Первый закон Коновалова выполняется и для реальных растворов.





рис. 5.6. Диаграммы «давление – состав» и «температура – состав» для реальных (неидеальных) бинарных летучих жидкостей
Как видно из рисунков с экстремумами, в точках экстремума кривые жидкости и пара соприкасаются, то есть состав жидкости и пара в точках экстремума одинаков.Этот вывод называется вторым законом Коновалова. В термодинамической теории растворов оба закона Коновалова теоретически обоснованы. Их обоснование приводится в параграфе 5.5. Смеси, соответствующие по составу точкам экстремума, называются азеотропными, или нераздельно кипящими. Они ведут себя при нагревании как один компонент, их нельзя разделить простой перегонкой.
Равновесие «жидкость – пар» часто удобнее рассматривать при условии постоянства давления. В этом случае диаграммы «температура – состав» характеризуют температуру кипения жидкостей в зависимости от состава (кривая жидкости) и равновесный состав насыщенного пара при температуре кипения жидкости (кривая пара). Диаграммы «температура – состав» приведены в нижнем ряду на рис. 5.6. При этом следует обратить внимание, что кривые жидкости и область жидкой фазы находятся в этом случае в нижней части диаграммы, а область пара и кривая пара – в верхней части.
Компонент, который более летуч, в данном случае компонент 2, имеет более высокое давление насыщенного пара Рº2 , чем первый, и более низкую температуру кипения.
5.5. Закономерности общего давления пара над смесью двух летучих жидкостей. Обоснование законов Коновалова
В предыдущих параграфах главы мы рассматривали жидкости, имеющие достаточно высокое давление собственного пара. Их называют летучими жидкостями. К смесям летучих жидкостей относятся, например, нефть и продукты её первичной переработки: бензин, керосин.
Рассмотрим двухкомпонентную жидкую летучую смесь с давлением паров над чистыми веществами  и
и  . Допустим, что оба компонента неограниченно растворимы друг в друге и смесь паров над идеальным раствором подчиняется законам идеальных газов. Допустим также, что
. Допустим, что оба компонента неограниченно растворимы друг в друге и смесь паров над идеальным раствором подчиняется законам идеальных газов. Допустим также, что  >
>  . Такая система, как мы уже знаем, подчиняется уравнению Дюгема – Маргулеса (5.13):
. Такая система, как мы уже знаем, подчиняется уравнению Дюгема – Маргулеса (5.13):
dlnP1 = -  dlnP2
dlnP2
По закону Дальтона,
 (5.29)
(5.29)
Молярные доли со штрихом относятся к фазе пара.
Из (5.13):
 , (5.30)
, (5.30)
откуда
(5.31)
Заменим  по уравнению (5.29)
по уравнению (5.29)
 (5.32)
(5.32)
Разделим левую и правую части (5.32) на dN2 :
(5.33)
Общее давление пара над смесью двух летучих жидкостей равно сумме парциальных давлений:
Р = Р1 + Р2 (5.34)
Возьмём производную по N2 от обеих частей уравнения (5.34):
(5.35)
Подставим в (5.35) значение dP1/dN2 из (5/33):
 (5.36)
(5.36)
где  называется коэффициентом разделения. Он зависит от состава смеси. Чем больше отличается состав смеси от состава равновесного с ней пара, тем больше α отличается от единицы и тем легче разделить летучую смесь на компоненты методом перегонки.
называется коэффициентом разделения. Он зависит от состава смеси. Чем больше отличается состав смеси от состава равновесного с ней пара, тем больше α отличается от единицы и тем легче разделить летучую смесь на компоненты методом перегонки.
Уравнение (5.36) является основным уравнением для неограниченно смешивающихся жидких бинарных летучих смесей. Проанализируем это уравнение. С ростом содержания компонента в растворе его парциальное давление всегда увеличивается, т.е. dP2/dN2 >0 и dP1/dN1 >0 , а общее давление пара над раствором с изменением состава раствора может как увеличиваться, так и уменьшаться.
Если общее давление пара над раствором увеличивается с ростом содержания второго компонента в растворе, т. е. dP/dN2 >0 то из уравнения (5.36):
 > 0 и
> 0 и  (5.37)
(5.37)
и поэтому
 , а
, а  (5.38)
(5.38)
И наоборот, если общее давление пара над раствором уменьшается с ростом молярной доли второго компонента N2, то
, а  (5.39)
(5.39)
Неравенства (5.38) и (5.39) выражают первый закон Коновалова, сформулированный нами ранее на основе анализа диаграмм, в параграфе 5.3.: «Пар над смесью двух летучих жидкостей относительно богаче тем компонентом, добавление которого к жидкости повышает общее давление над раствором при постоянной температуре или понижает температуру кипения раствора при постоянном давлении».
Если на кривой Р=f(N2) имеется экстремум, то в точке экстремума
dP/dN2=0 (5.40)
Тогда, из (5.36) получим:
 =0 и
=0 и  (5.41)
(5.41)
Отсюда получим, что в точке экстремума

 (5.42)
(5.42)
Соотношения (5.42) являются теоретическим обоснованием второго закона Коновалова, сформулированного на основе анализа диаграмм в параграфе 5.4.: «Точки экстремума на кривых общее давление пара – состав раствора или на кривых температура кипения – состав раствора отвечают растворам, состав которых одинаков с составом равновесного с ним пара».
5.6. Разделение жидких бинарных летучих смесей перегонкой
Простейшая установка для перегонки жидких летучих смесей показана на рис. 5.7.
Разделение смесей осуществляют следующим образом. Пусть исходная жидкость имела состав «а» (см. рис. 5.8). Нагреем жидкость до температуры кипения в условиях Р=const. Этот процесс характеризует вертикальная пунктирная линия, выходящая из точки «а». Её пересечение с кривой жидкости (нижняя линия на диаграмме) характеризует температуру кипения жидкости состава «а». При температуре кипения жидкости образуется пар состава «а΄». Будем отводить пар, конденсируя его в холодильнике, как показано на рис. 5.7. В соответствии с первым законом Коновалова, в паре больше летучего, легкого, низкокипящего (в данном случае 1-го) компонента, по сравнению с кипящей жидкостью исходного состава. Это видно по взаимному расположению точек «а» и «а΄».

Рис. 5.7. Установка для простой перегонки летучих жидкостей.
1- штатив; 2 – нагреватель (пламя спиртовки показано условно, на практике – это нагревательный элемент закрытого типа); 3 – колба с перегоняемой жидкостью; 4 – холодильник( он состоит из внутренней трубки, в которой конденсируется перегоняемая жидкость, и внешней «рубашки», через которую пропускают охлаждающую жидкость, чаще всего воду); 5 – колба – приёмник, в которую стекает конденсат
Следовательно, жидкость в процессе перегонки обогащается более тяжёлым (в данном случае вторым) компонентом и её температура кипения поэтому повышается (направление стрелки на кривой жидкости). Например, до точки «в». Пар при этом имеет состав «в΄». Если перегонку закончить на этом, то получим остаток состава «в» и конденсат какого-то среднего состава  между составом «а΄» и «в΄». В остатке, таким образом, мы получили жидкость, обогащенную тяжелым компонентом (то есть вторым), а в конденсате, - летучим (то есть первым), по сравнению с исходной жидкостью. Если теперь провести перегонку повторно, используя в качестве исходной жидкости, конденсат состава
между составом «а΄» и «в΄». В остатке, таким образом, мы получили жидкость, обогащенную тяжелым компонентом (то есть вторым), а в конденсате, - летучим (то есть первым), по сравнению с исходной жидкостью. Если теперь провести перегонку повторно, используя в качестве исходной жидкости, конденсат состава  , то получим вторичный конденсат, очень близкий по составу к чистому первому компоненту. Так, повторяя перегонку несколько раз с использованием очередного конденсата, можно получить в приёмнике практически чистый летучий компонент, а в остатке, если его использовать далее, - чистый второй, т.е. тяжёлый компонент.
, то получим вторичный конденсат, очень близкий по составу к чистому первому компоненту. Так, повторяя перегонку несколько раз с использованием очередного конденсата, можно получить в приёмнике практически чистый летучий компонент, а в остатке, если его использовать далее, - чистый второй, т.е. тяжёлый компонент.

Рис. 5.8. Принципиальная схема разделения смесей на компоненты
При разделении жидких бинарных летучих смесей, образующих азеотроп (рис. 5.6), методом простой перегонки можно выделить в чистом виде только один компонент. Так, в условиях Р=const (нижний ряд рисунков), в конденсате в чистом виде можно получить то, что кипит при более низкой температуре. На диаграммах с минимумом в конденсате конечной точкой перегонки будет являться азеотроп, а в остатках либо первый (если исходная смесь имеет до-азеотропный состав), либо второй (если исходная смесь за-азеотропного состава) компоненты. На диаграммах с максимумом, наоборот: в конденсате первый или второй компоненты, а в остатке – азеотроп.
Этот же принцип лежит в основе разделения многокомпонентных жидких летучих смесей. Только в таком случае разделение происходит на фракции. Каждая фракция имеет определенный диапазон температур кипения. Перегонка широко применяется в нефтепереработке. Там эти процессы осуществляются непрерывно, в ректификационных колоннах. На разных уровнях по высоте колонны поддерживаются разные температурные режимы: на более высоких уровнях конденсируются самые лёгкие углеводороды, на средних – более тяжёлые, а самые высококипящие – на нижних. Нефть подаётся в колонну снизу, нагретая в печах до 350 градусов. А из колонны выходят сырьевые продукты бензиновых, керосиновых фракций, и более тяжёлые – лигроин, и, в качестве остатка, - мазут. Каждая из этих фракций представляет собой смесь углеводородов, близких по температурам кипения. Это лишь один из возможных вариантов ректификации. Вторичная перегонка позволяет разделить каждую из полученных фракций на ещё более узкие.
5.7. Осмотическое давление
Осмосом называют самопроизвольное проникновение растворителя через полупроницаемую перегородку в раствор. Полупроницаемой перегородку называют потому, что через неё могут проходить только молекулы растворителя, а растворенного вещества – не могут. Сила, заставляющая молекулы растворителя переходить через полупроницаемую перегородку (мембрану), названа осмотическим давлением. Его можно иначе определить как давление, которое необходимо приложить, чтобы прекратить переход растворителя через мембрану. Впервые осмотическое давление было обнаружено Нолле, в 1748 году.
Простейший осмометр изображен на рис. 5.9. Сосуд 2 с водным раствором снизу закрыт мембраной и помещен в сосуд 1, наполненный водой. Вода вследствие осмоса проникает в сосуд 2. Гидростатическое давление столба жидкости в сосуде 2 уравновесит осмотическое давление и установится равновесие.
В 1887 году Вант-Гофф показал, что осмотическое давление π в разбавленных растворах выражается уравнением:
π = СRT (5.43)
Для идеальных растворов уравнение Вант-Гоффа можно получить, исходя из условия равенства химических потенциалов растворителя в растворе μ1 и в чистом растворителе μ01 .

|
Это равенство – есть условие установившегося равновесия в системе:
μ1(N1, π) = μ01 (5.44)
Возьмем полный дифференциал от обеих частей уравнения (5.44), учитывая, что химический потенциал чистого растворителя – постоянная величина.
Рис. 5.9. Осмометр
 (5.45)
(5.45)
Применяя полученные ранее уравнения для характеристических функций (2.61), с учетом тождества (2.68), можно записать:
 , (5.46)
, (5.46)
где  - парциальный молярный объём растворителя.
- парциальный молярный объём растворителя.
Подставляя (5.46) в (5.45), получим уравнение, устанавливающее зависимость осмотического давления от состава раствора и химического потенциала растворителя:
 (5.47)
(5.47)
В идеальном раствореизменения объёма компонента при образовании растворане происходит,поэтому парциальный молярный объём растворителя равен молярному объёму чистого растворителя  , а
, а  выражается уравнением(2.75). С учетом этого из (5.47) получим:
выражается уравнением(2.75). С учетом этого из (5.47) получим:
 (5.48)
(5.48)
В результате интегрирования уравнения (5.48) в пределах от 0 до  и от 1 до N1, получим уравнение, выражающее зависимость осмотического давления идеального раствора от состава:
и от 1 до N1, получим уравнение, выражающее зависимость осмотического давления идеального раствора от состава:
 (5.49)
(5.49)
Для предельно разбавленных растворов уравнение (5.49) тоже применимо. Учитывая, что
–lnN1 = - ln(1-N2) ≈ N2 , (5.50)
а молярный объём чистого растворителя равен молярному объёму раствора V, из (5.49) получим:
 или , (5.51)
или , (5.51)
где С – концентрация раствора.
Осмотическое давление играет очень важную роль в процессах жизнедеятельности различных организмов. По закону осмоса происходит распределение различных веществ и воды в тканях человека и животных. Известно, что осмотическое давление крови человека составляет около 8 атм (8,1·105 Па). Недостаток воды в организме проявляется чувством жажды, а утоление её восстанавливает необходимое осмотическое давление крови и восстанавливает водно-солевой баланс. Осмотическое давление служит движущей силой для поглощения влаги прорастающими в почве семенами, благодаря чему, даже при невысокой окружающей влажности, «сосущая сила клетки» может достигать нескольких сотен атмосфер. На применении уравнения Вант-Гоффа основан один из методов определения молярной массы растворенного вещества в разбавленном растворе.
5.8. Взаимная растворимость жидкостей
По взаимной растворимости жидкости условно делят на 3 группы:
1) взаимно не растворимые (например, ртуть и вода);
2) неограниченно растворимые (например, вода и ацетон);
3) ограниченно растворимые (например, вода и анилин).
Рассмотрим системы с ограниченной взаимной растворимостью компонентов.
 |
Взаимная растворимость компонентов зависит от температуры. Эта зависимость на диаграмме состояния изображается в виде кривой расслоения (рис. 5. 10).
Рис. 5.10. Диаграмма состояния системы вода – анилин
Область ограниченной растворимости компонентов находится на рис. 5.10 под кривой расслоения АВС. В любой точке под кривой система гетерогенна и состоит из двух сопряженных растворов: раствор анилина в воде и раствор воды в анилине. Составы сопряженных фаз находят по кривой расслоения: кривая. АВ характеризует состав водного слоя в зависимости от температуры, а кривая ВС – анилинового.
С ростом температуры взаимная растворимость компонентов растет, и при температуре, соответствующей точке В (критическая точка), составы слоёв становятся одинаковы и они сливаются, образуя однофазную двухкомпонентную систему, состав которой характеризует проекция точки В на ось абсцисс. За пределами заштрихованной области расслоения система гомогенна, то есть представляет собой либо раствор анилина в воде, либо раствор воды в анилине, в зависимости от того, какой из компонентов преобладает в составе раствора (это растворитель), а какой находится в виде растворенного в нём вещества.
Составы сопряженных слоёв и их относительные количества можно найти по правилу рычага. Допустим, взято 5 кг смеси. Обозначим массу слоя «n» за х, тогда масса слоя «l» будет равна 5-х. По правилу рычага, х/(5-х) = Мl/Мn. Допустим, отношение отрезков составляет 0,8. Тогда х=(5-х)0,8 , откуда х=2,2 кг. Определив по диаграмме относительные содержания компонентов в каждом слое, (проекции точек n и l на ось состава), можно найти количество каждого компонента в анилиновом и водном слоях.
Существуют системы с нижней критической точкой расслоения, например, система вода – триэтиламин (кривая, ограничивающая область расслоения, проходит в этом случае через минимум), а также с двумя критическими точками: верхней и нижней (например, вода – никотин).
Существование верхней и или нижней критических температур расслоения находится в соответствии с принципом смещения равновесия Ле Шателье – Брауна. Если процесс взаимного растворения двух жидкостей сопровождается поглощением теплоты, то нагревание будет увеличивать взаимную растворимость. В этом случае будет существовать верхняя критическая точка. В экзотермическом процессе растворения картина будет противоположная: если процесс взаимного смешения жидкостей сопровождается выделением тепла, то понижение температуры будет повышать взаимную растворимость, и на кривой расслоения будет наблюдаться минимум. Существование двух критических точек расслоения говорит о том, что с изменением температуры происходит смена знака теплоты растворения.
Большое значение имеют вопросы взаимной растворимости жидкостей в образовании металлургических сплавов. Существуют металлы, взаимная растворимость которых в расплавленном состоянии очень мала. Например, практически не растворимы друг в друге расплавленные железо и свинец. При температуре выше 15270 ±50 они будут существовать в виде двух жидких слоев. При понижении температуры система будет представлять собой сначала твердое железо и расплавленный свинец, а затем, при температуре ниже 3270, когда будет достигнута температура кристаллизации свинца, образуется 2 слоя твердых фаз, состоящих из практически чистых металлов. Растворимость Fe в Pb в твердом состоянии равна 2·10-4 вес.%.
Явления расслаивания очень важны в геологии. Они проявляются, например, при образовании магматических пород. В основных и ультраосновных магмах при высоких концентрациях серы, меди, никеля и железа явления расслаивания вызывают кристаллизацию пирротина FeS, пентландита (Fe, Ni)9S8, пирита FeS2, халькопирита CuFeS2 и других минералов из сульфидного расплава. Это приводит, например, к формированию крупных медно – никелевых месторождений (Норильск, Талнах).
5.9. Закон распределения Нернста. Экстракция
Рассмотрим систему, состоящую из двух практически не растворимых друг в друге жидкостей. Если к такой системе добавить третью жидкость, которая растворима и в первом, и во втором растворителях, то распределение третьего компонента между двумя несмешивающимися жидкостями будет происходить в соответствии с законом распределения Нернста: «В равновесной гетерогенной системе, состоящей из двух нерастворимых или ограниченно растворимых жидкостей, отношение концентраций третьего компонента, распределяющегося между ними, есть величина постоянная, зависящая только от температуры»:
(5.52)
К* – коэффициент распределения, зависящий от природы веществ и от температуры. Закон распределения Нернста выполняется в виде уравнения (5.52) при условии отсутствия диссоциации и ассоциации молекул распределяющегося компонента и отсутствии его влияния на взаимную растворимость 1-го и 2-го растворителей. Например, при распределении янтарной кислоты С2Н4(СООН)2 между этиловым спиртом (2) и водой (1), она практически не диссоциирует в них и К*=5,38 при 298 К.
В общем случае:
 (5.53)
(5.53)
При ассоциации молекул растворенного вещества n и m меньше единицы, при диссоциации – больше единицы. Так, например, при распределении салициловой кислоты, С6Н4(ОН)СООН, между водой (1) и бензолом (2) при 298 К , происходит её частичная диссоциация в воде, и закон распределения для этой системы выразится уравнением:  .
.
Закон распределения можно обосновать теоретически, учитывая, что равновесие растворенного вещества в двух несмешивающихся растворителях характеризуется равенством его химических потенциалов в обеих фазах:
 , (5.54)
, (5.54)
откуда:
 (5.55)
(5.55)
Так как стандартные химические потенциалы веществ,  , а также R и T – постоянны, то и отношение активностей компонента 3 в первом и втором растворителях постоянно, т.е.
, а также R и T – постоянны, то и отношение активностей компонента 3 в первом и втором растворителях постоянно, т.е.
(5.56)
Выразим активности через коэффициенты активностей f и концентрации C:
 (5.57)
(5.57)
очевидно, что соотношение констант К и К* выражается уравнением:
 (5.58)
(5.58)
Строго говоря, формальный коэффициент распределения К* зависит от концентрации растворенного вещества в обоих растворителях, поскольку коэффициент активности f зависит от концентрации веществ. С разбавлением, когда f →1, К перестает зависеть от концентрации и становится равен К.
На законе распределения Нернста основан метод извлечения растворенного вещества из раствора при помощи второго растворителя.
Этот метод называется экстракцией. Рассмотрим некоторые закономерности процесса экстракции.
Представим себе раствор, состоящий из двух жидкостей: растворителя и растворенного вещества, общим объёмом V1 (объём экстрагируемого раствора). Допустим, необходимо извлечь растворённое вещество. Добавим к нему некоторый объём другого растворителя (экстрагента) V2, не смешиваемого с первым. Часть растворенного вещества перейдет во второй растворитель, т. е произойдет экстракция. При необходимости извлечения растворенного вещества, подбирают экстрагент, в котором данное вещество растворимо намного лучше, чем в исходном растворителе. По закону распределения, отношение равновесных концентраций растворенного вещества во втором и первом растворителях: К=С2/С1. Допустим, в первом растворителе после экстракции осталось количество растворенного вещества g1, а во второй растворитель перешло количество вещества go – g1. Тогда:
 , (5.59)
, (5.59)
где go – количество растворённого вещества в первом растворителе до экстракции. Количество вещества, оставшееся в первом растворителе после экстракции, найдем из уравнения 5.59:
(5.60)
Для более полного извлечения вещества повторим экстракцию с новой порцией второго растворителя, добавив его к объёму раствора, оставшегося после первой экстракции. После повторной экстракции в исходном растворителе останется неизвлеченного вещества:
(5.61)
После «n» экстракций количество оставшегося в первом растворителе вещества будет
 (5.62)
(5.62)
Если экстракцию провести однократно, использовав сразу весь объём растворителя, nV2 , то количество оставшегося, неэкстрагированного вещества в первом растворителе будет
 (5.63)
(5.63)
Сравнение уравнений (5.62) и (5.63) показывает, что, поскольку степенная функция (5.63) убывает быстрее, чем линейная (5.64), очевидно, что количество оставшегося неизвлеченного вещества в первом растворителе будет гораздо больше при однократном использовании растворителя, g/ . Следовательно, более полное извлечение растворенного вещества достигается при многократной экстракции малыми порциями экстрагента.
5.10. Растворимость твердых веществ в жидкостях
Растворимость твердого вещества в жидкости зависит от природы растворяемого вещества и растворителя, от давления и температуры, а также от присутствия других веществ в растворе, особенно электролитов. Растворимость твердых веществ в одном и том же растворителе варьируется в очень широких пределах. В качестве примеров, приведем растворимость ряда неорганических веществ в воде при стандартных условиях, (таблица 5.1)
Таблица 5.1
| Вещество | AgNO3 | AlCl3 | Ag2CO3 | Fe(OH)2 | AgJ |
| Растворимость, в г на 100г воды | 249,6 | 45,1 | 3,3·10-8 | 6,2·10-5 | 2,3·10-7 |
Зависимость растворимости от природы растворителя также весьма существенна. Так, например, растворимость ромбической серы, в г на 100 г растворителя, в С6H 6 – 2,5, а в CCl4 – 0,84. Известно, что полярные вещества, как правило, лучше растворяются в полярных растворителях, а неполярные – в неполярных.
Растворимость твердых веществ в смешанных растворителях зависит от соотношения компонентов растворителя. Так, например, растворимость КNO3 в водном растворе этилового спирта при 298 К составляет 23,5 г на 100 г растворителя в 10%-ном растворе С2Н5ОН и 1,35 г в 70%-ном растворе.
Растворимость твёрдых веществ в жидкостях зависит от температуры.
Рассмотрим систему, представляющую собой идеальный насыщенный раствор соли в равновесии с той же солью в твёрдом состоянии. Равновесие твёрдого растворённого вещества с его насыщенным раствором при данной температуре и постоянном давлении характеризуется равенством химических потенциалов растворённого вещества в насыщенном растворе, μ2, и чистого твёрдого растворённого вещества, μº2:
μ2(N2нас,Т) = μº2(Т), (5.64)
где N2нас – концентрация растворённого вещества в насыщенном растворе.
Возьмём полный дифференциал от обеих частей этого равенства:
 (5.65)
(5.65)
По аналогии с уравнением (2.61):

можно записать
 и
и  (5.66)
(5.66)
где  - парциальная молярная энтропия растворённого вещества в растворе данного состава;
- парциальная молярная энтропия растворённого вещества в растворе данного состава;
 - энтропия 1 моля этого же вещества в твёрдом состоянии.
- энтропия 1 моля этого же вещества в твёрдом состоянии.
Отсюда
 , (5.67)
, (5.67)
где  - изменение парциальной молярной энтропии растворенного вещества при образовании насыщенного раствора, которое равно разности энтропий вещества в насыщенном растворе (конечное состояние) и в твёрдом состоянии (начальное состояние вещества);
- изменение парциальной молярной энтропии растворенного вещества при образовании насыщенного раствора, которое равно разности энтропий вещества в насыщенном растворе (конечное состояние) и в твёрдом состоянии (начальное состояние вещества);
 – концентрация растворённого вещества в насыщенном растворе.
– концентрация растворённого вещества в насыщенном растворе.
Преобразуем уравнение (5.67) к виду:
(5.68)
Для идеального раствора:
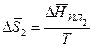 (5.69)
(5.69)
Поясним это выражение. По закону Гесса, растворение можно представить как последовательную совокупность двух процессов: плавление твёрдого вещества и последующее растворение жидкости в идеальном растворе. Так как теплота растворения жидкости в идеальном растворе равна нулю, то теплота растворения равна теплоте плавления вещества.
Подставим изменение энтропии (5.69) в уравнение (5.68):
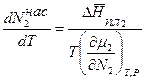 , (5.70)
, (5.70)
где 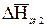 - дифференциальная теплота растворения вещества 2 в растворе данного состава.
- дифференциальная теплота растворения вещества 2 в растворе данного состава.
В идеальном растворе
μ2=μº2 + RTlnN2 и dμ2 = RTdlnN2 или 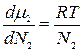 (5.71)
(5.71)
Подставив значение производной (5.71) в уравнение (5.70), получим:
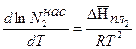 (5.72)
(5.72)
Уравнение (5.72) называют уравнением Шредера, оно устанавливает зависимость растворимости твёрдого вещества в растворе от температуры. Из уравнения видно, что поскольку теплота плавления - величина положительная, то с ростом температуры растворимость твёрдого вещества в идеальном растворе возрастает, т.к. 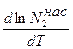 >0. Проинтегрируем уравнение (5.72) в пределах от 1 до N2 и от
>0. Проинтегрируем уравнение (5.72) в пределах от 1 до N2 и от 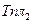 до Т, считая теплоту плавления постоянной в данном интервале температур:
до Т, считая теплоту плавления постоянной в данном интервале температур:
 (5.73)
(5.73)
Из уравнения (5.73) следует, что растворимость твердого вещества в идеальном растворе не зависит от природы растворителя.
Проинтегрируем уравнение Шредера (5.72) с константой интегрирования:
, (5.74)
где const – постоянная интегрирования. Из уравнения (5.74) следует, что зависимость  от 1/Т линейна. Из углового коэффициента прямой в данных осях координат можно определить теплоту плавления вещества, а экстраполируя прямую до
от 1/Т линейна. Из углового коэффициента прямой в данных осях координат можно определить теплоту плавления вещества, а экстраполируя прямую до  =0, можно найти температуру плавления расворенного вещества.
=0, можно найти температуру плавления расворенного вещества.
Для неидеальных растворов зависимость выражают через активность растворенного вещества:
 (5.75)
(5.75)
Для интегрирования уравнения (5.75) необходимо знать зависимость активности растворенного вещества, а2, и дифференциальной теплоты его растворения, , от состава.
Для большинства кристаллических веществ растворение сопровождается поглощением тепла, поэтому растворимость твердых веществ с ростом температуры возрастает.
5.11. Понижение температуры замерзания и повышение температуры кипения растворов
Понижение температуры замерзания – это разность между температурой замерзания растворителя и раствора:
ΔТз = Тз1 – Тз (5.76)
Повышение температуры кипения – это разность между температурой кипения раствора и растворителя:
ΔТк = Тк – Тк1 (5.77)
Для разных типов растворов зависимости ΔТз и ΔТк от состава раствора различны. Рассмотрим эти зависимости.
А) Идеальные растворы
Если при температуре замерзания (или плавления) в твёрдую фазу из раствора выделяется только растворитель, то равновесие в системе характеризуется равенством химических потенциалов μ1 растворителя в растворе и μ1о чистого твёрдого растворителя
μ1(N1, Tз) = μ1о(Тз) (5.78)
Возьмем полный дифференциал левой и правой части (5.78):
 (5.79)
(5.79)
По аналогии с (2.61), учитывая тождество химического потенциала и парциального мольного изобарного потенциала, применим далее соотношения:
 и (5.80)
и (5.80)
где  - парциальная молярная энтропия растворителя в растворе данного состава;
- парциальная молярная энтропия растворителя в растворе данного состава;  - молярная энтропия чистого твердого растворителя. Введя обозначения (5.80) в (5.79), получим:
- молярная энтропия чистого твердого растворителя. Введя обозначения (5.80) в (5.79), получим:
 (5.81)
(5.81)
где  - изменение парциальной молярной энтропии растворителя при образовании раствора, которое можно выразить, с учетом (2.10), через дифференциальную теплоту растворения твердого растворителя в растворе данного состава при температуре замерзания:
- изменение парциальной молярной энтропии растворителя при образовании раствора, которое можно выразить, с учетом (2.10), через дифференциальную теплоту растворения твердого растворителя в растворе данного состава при температуре замерзания:
 (5.82)
(5.82)
Подставляя (5.82) в (5.81), получим
 (5.83)
(5.83)
В уравнении (5.83) и далее перешли к значкам полного дифференциала температуры замерзания по составу, N1, так как давление слабо влияет на равновесие в растворах.
Учитывая, [из (5.17)], что
 , (5.84)
, (5.84)
а также обоснованное ранее (см. параграф 5.10) равенство для идеальных растворов теплоты растворения теплоте плавления:
 , (5.85)
, (5.85)
получим для идеального раствора:
 (5.86)
(5.86)
Проинтегрировав в пределах от 1 до N1 и от Тз1 до Тз, получим зависимость понижения температуры замерзания идеального раствора от состава:
 , (5.87)
, (5.87)
где ΔНºпл1 – теплота плавления чистого растворителя; N1 – мольная доля растворителя в растворе.
Из уравнения (5.87) видно, что чем меньше мольная доля растворителя, т.е. чем больше N2 – мольная доля растворенного вещества, тем ниже температура замерзания раствора.
Если при температуре замерзания раствора Тз в твердую фазу выделяются оба компонента, то
 , (5.88)
, (5.88)
где N1(ж) – молярная доля растворителя в жидком растворе;
N1(тв) – молярная доля растворителя в твердом растворе.
Если N1(ж) > N1(тв) , то Тз раствора может быть выше, чем Тз1.
Зависимость температуры кипения Тк от состава идеального раствора описывается подобными уравнениями:
 , (5.89)
, (5.89)
где  , т.е. с увеличением мольной доли растворенного вещества (N1 уменьшается), температура кипения раствора Тк повышается.
, т.е. с увеличением мольной доли растворенного вещества (N1 уменьшается), температура кипения раствора Тк повышается.
Интегрируя в пределах от 1 до N1 и от Тк1 до Тк , получим:
(5.90)
где  – теплота испарения чистого растворителя.
– теплота испарения чистого растворителя.
Так как lnN1 < 0, то ΔТк > 0 , т.е. температура кипения раствора Тк выше, чем чистого растворителя Тк1. При этом второй компонент раствора считается нелетучим.
Б)Предельно разбавленные растворы
В предельно разбавленных растворах уравнения (5.87) и (5.90) применимы только для растворителя. Введём ряд упрощений, справедливых для предельно разбавленных растворов:
Тз≈Тз1, Тк≈Тк1, Тз1Тз≈Т2з1 и Тк1Тк≈Т2к1 , (5.91)
а также будем считать число молей раствора равным числу молей растворителя:
(5.92)
где m – моляльная концентрация раствора.
Тогда молярная доля растворенного вещества приближенно равна моляльности, отнесенной к числу молей растворителя:
 (5.93)
(5.93)
Учтем также, что - lnN1= - ln(1-N2) , а при очень малых N2, разложение в ряд функции ln(1-N2) позволяет ограничиться первым слагаемым:
ln(1-N2)≈-N2 . (5.94)
При подстановке (5.93) в (5.92) получим:
 (5.95)
(5.95)
Подставим (5.91) и (5.95) в уравнения (5.87) и (5.90). Получим уравнения, выражающие понижение температуры замерзания и повышение температуры кипения предельно разбавленных растворов:
ΔТз = К·m (5.96)
ΔTк = Е·m (5.97)
где m – моляльная концентрация растворенного вещества;
К – криоскопическая постоянная;
Е – эбуллиоскопическая постоянная.
 , град/моль (5.98)
, град/моль (5.98)
 , град/моль (5.99)
, град/моль (5.99)
Физический смысл констант К и Е определяется уравнениями (5.96) и (5.97): константаК численно равна понижению температуры замерзания раствора с моляльностью m равной 1;
константа Е численно равна повышению температуры кипения раствора с моляльностью m равной 1. Как видно из уравнений (5.98) и (5.99), эти константы зависят только от свойств растворителя и не зависят от природы растворенного вещества. Величины этих констант определяются экстраполяцией при m→ 0 отношений:
;  (
(






